Un réseau circulaire d'absorption ou de phase qui focalise la lumière incidente est appelé une plaque de zone de Fresnel (FZP, Fig. 1) [Fre 1866]. En 2008, le plus petit diamètre de focalisation de la lumière des rayons X obtenu avec cette plaque était de 15 nm. Il y a des plaques de zone de transmission et de réflexion.
Les plaques de zone Fresnel peuvent être divisées en plusieurs types :
| Plaque de zone de Fresnel de réflexion | Plaques de zone condenseur |
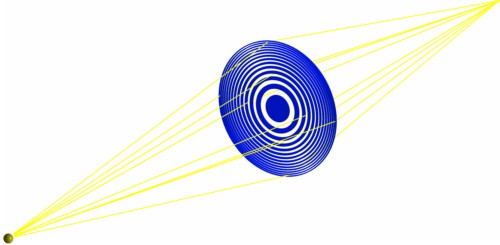
Fig. 1 : Mise au point des rayons X avec une plaque de zone de Fresnel
Tout comme pour la lumière visible, il existe des plaques de zone de Fresnel absorbantes ou déphasantes pour les rayons X. Les plaques de zone absorbante sont plus courantes dans le domaine des rayons X. Ils sont constitués d'une membrane transparente aux rayons X (par exemple Si3N4) qui porte les structures absorbantes (par exemple quelques micromètres d'or) de la plaque de zone. Normalement, les structures métalliques absorbantes sont produites par dépôt galvanique dans une structure de résist préalablement structurée par un faisceau d'électrons ou d'ions.
Le tableau 1 donne un aperçu des paramètres les plus importants des plaques de zone de Fresnel, situation en 2009.
| Paramètre | Symbole |
Valeurs typiques |
|
| plaque microzone | plaque de zone condenseur | ||
| Diamètre | D | <0.1 mm | <10 mm |
| Distance focale | f | 0.5-1.5 mm | <20 mm |
| Nombre de zones | N | 100-1000 | <50.000 |
| Largeur de zone la plus petite | 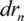 |
15-50 nm | 30-50 nm |
| Résolution spatiale (critère de Rayleigh) | 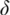 |
1.22 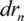 nm nm |
|
| Efficacité de diffraction | 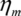 |
(5...30)% | |
Tableau 1 : Paramètres typiques des plaques de zone de Fresnel de transmission [VDI 2009c].
Comme il est techniquement très exigeant de produire les bagues extérieures fines d'une plaque de zone, des plaques de zone composites sont également utilisées. Il s'agit d'une plaque de zone intérieure utilisée dans le premier ordre de diffraction et d'une plaque de zone extérieure utilisée dans le deuxième ordre de diffraction (Fig. 2). Les structures des bords de la plaque de zone extérieure ne sont pas aussi fines en raison de l'utilisation du deuxième ordre de diffraction et sont donc plus faciles à fabriquer.

Fig. 2 : Plaque de zone composite avec des plaques de zone intérieure et extérieure utilisées respectivement dans le premier et le deuxième ordre de diffraction.
Calcul des plaques de zone de Fresnel
La largeur des anneaux drn du reseau circulaire d'une plaque de zone diminue au fur et à mesure que le rayon rn des anneaux augmente. Les rayons des anneaux peuvent être calculés pour une lumière monochromatique de longueur d'onde à émettre à partir d'une source ponctuelle Q et focalisée sur un point P à distance g + b = nλ, avec un nombre naturel n, la largeur d'objet g et la largeur d'image b [Sor 1875]. Pour chaque trajet optique de la source au point focal en passant par la plaque de zone, la lumière doit interférer de manière constructive. La figure 3 montre le trajet optique d'un faisceau qui frappe la plaque de zone à une certaine distance rn de l'axe optique.
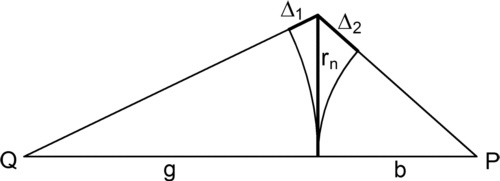
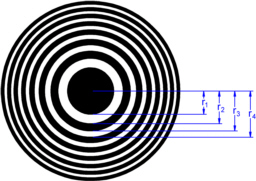
Fig. 3 : Schéma de la différence de longueur du trajet optique entre le point source Q et le point focal P à une distance rn du faisceau de l'axe optique
Les différences de longueur du chemin optique sont les suivantes
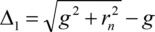
et
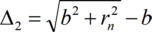
la lumière qui passe par les zones voisines interférera de façon destructive. Lorsque maintenant une zone sur deux absorbe les rayons X, la lumière passant par les zones transmissives d'une plaque de zone de Fresnel aura une différence de chemin optique de nλ et donc interférera de manière constructive dans le point focal P. La réorganisation de cette formule donne les résultats suivants
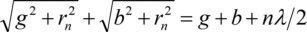
ou au carré
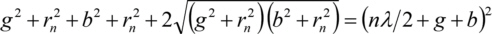
Après réarrangement, mise au carré et séparation rn, le rayon de la nième zone de Fresnel est le suivant
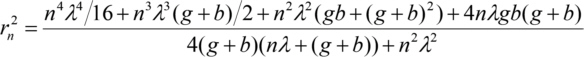
Comme λ est petit comparé à b et g, négliger tous les termes d'ordre supérieur dans λ et utiliser nλ<<g+b est une bonne approximation.

La distance focale d'une plaque de zone de Fresnel dépend donc de la longueur d'onde. Dans la dernière étape, on a utilisé l'équation de la distance focale f d'un objectif mince :
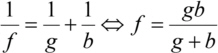
La dérivation du rn approximatif à n donne la largeur drn du nième anneau.
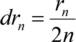
La surface de chacun des anneaux de la plaque de zone est constante à longueur d'onde et longueur focale constantes à travers la plaque de zone. Cela signifie que chaque zone apporte la même intensité à la mise au point.
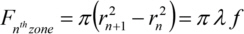
Les réseaux ont généralement plus d'un ordre de diffraction. Une plaque de zone de Fresnel a donc généralement plusieurs points focaux (Fig. 4 à gauche). Les ordres de diffraction négatifs conduisent à des faisceaux divergents ou en d'autres termes : les plaques de zone se comportent également comme des lentilles de diffusion avec des points focaux virtuels. Si une plaque de zone est utilisée comme lentille de mise au point, seul le premier ordre de diffraction est normalement utilisé et tous les autres ordres de diffraction doivent être supprimés par des apertures appropriées (figure 4 de droite).
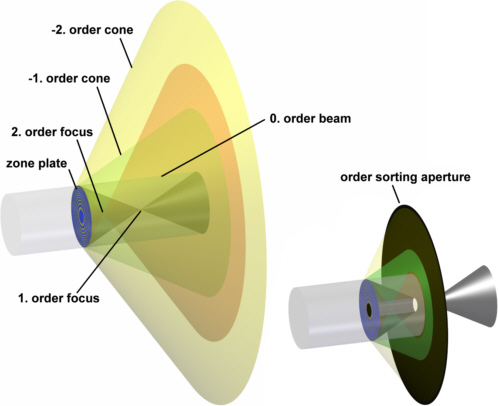
Fig. 4 : Ordres de diffraction d'un réseau circulaire (à gauche) ; avec apertures pour supprimer les autres ordres de diffraction (à droite) ; les faisceaux du premier ordre de diffraction sont marqués en rouge lorsque la souris survole l'image. 
Efficacité des plaques de zone Fresnel
En raison de leur absorption, les plaques de zone absorbantes n'ont parfois que la moitié de la transmission comme plaques de zone avec de phase. La lumière, qui est due à des ordres de diffraction inutilisés, est perdue pour l'utilisation. L'efficacité de diffraction ηm du mème ordre de diffraction d'une plaque de zone est définie comme suit
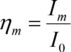
avec l'intensité de l'incident I0 et l'intensité dans le mème ordre de diffraction Im. Techniquement, des efficacités de 5 à 30% sont atteintes pour m = 1.
Une plaque de zone avec réseau d'absorption n'atteint l'efficacité de diffraction théoriquement possible que si l'épaisseur des structures absorbantes est suffisante pour absorber presque 100% de la lumière qui tombe sur les structures absorbantes. Si l'on utilise de l'or comme matériau absorbant et qu'il faut par exemple atteindre une absorption de 90%, l'épaisseur nécessaire de l'absorbeur dépendant de l'énergie photonique correspond à la ligne verte de la figure 5.
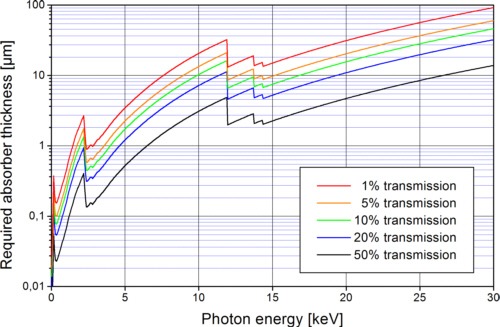
Fig. 5 : Epaisseur de l'absorbeur d'or nécessaire pour absorber la plus grande partie de la lumière incidente sur les structures de l'absorbeur
Selon la théorie d'Abbe, la résolution spatiale dZP d'une plaque de zone de Fresnel dépend de l'aperture numérique NAE, ZP de la plaque de zone
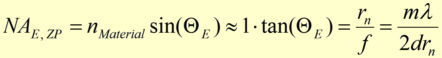
avec l'indice de réfraction nmatière (= partie réelle de l'indice de réfraction n*) du médium entre l'objet et la plaque de zone, l'angle de réception ΘE de la plaque de zone et l'ordre de diffraction m utilisé. On suppose approximativement que l'angle ΘE est normalement petit et que l'indice de réfraction est proche d'un. Selon le critère de Rayleigh, qui indique la résolution de deux points adjacents à l'aide d'une lentille à aperture numérique NA, on peut calculer la résolution spatiale δZP la plus grande théoriquement possible pour un éclairage incohérent et monochromatique comme étant
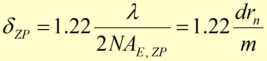
Les structures absorbantes d'une plaque de zone sont généralement produites par galvanoplastie d'or sur un substrat préalablement microstructuré. Le rapport d'aspect des microstructures est défini comme le rapport de la hauteur de la structure à la plus petite largeur de la structure. Le rapport d'aspect le plus élevé pour de telles structures en 2019 était d'environ 120 pour le procédé LIGAprocédé LIGA. Cela signifie que si la transmission admissible des structures de l'absorbeur peut être une valeur relativement élevée de 50% par exemple et que le rapport d'aspect du procédé utilisé est de 100 par exemple, des plaques de zone pour un rayonnement de 10 keV avec une focale minimale d'environ 40 nm peuvent être produites (figure 6). Pour obtenir des diamètres de mise au point plus petits ou la même taille de mise au point pour des énergies photoniques plus élevées, il faut soit améliorer le rapport d'aspect, soit diminuer l'efficacité de la plaque de zone en raison de la transparence croissante des structures absorbantes.
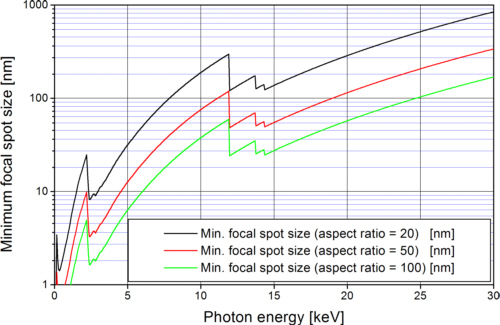
Fig. 6 : Diamètre de focalisation minimal théoriquement réalisable si l'on tolère une transmission des absorbeurs de 50%.
Plaques de zone de Bragg-Fresnel réfléchissantes
XXX
Le tableau 2 donne un aperçu des paramètres typiques des plaques de zone réfléchissantes de Fresnel, situation en 2009.
| Paramètre | Symbole |
Unité | Valeurs typiques |
|
| Plaque de zone réfléchissante TER | Plaque de zone réfléchissante Bragg-Fresnel | |||
| Distance de l'objet | g | mm | ∞-0.1 | ∞-3 |
| Distance de l'image | b | mm | 0.1-∞ | 3-∞ |
| Gamme d'énergie photonique | Ephoton | keV | 0.01-1 | 1-100 |
| Angle d'incidence | ΘZP | rad | 0.001-0.25 | 0.1-pi/2 |
| Largeur minimale des zones | ΔZP | nm | 1000 | 200 |
| Aperture numérique horizontale | NAhorizontal | rad | 0.01-0.25 | 0.01-0.25 |
| Aperture numérique verticale | NAvertical | rad | 0.1-0.9 | 0.01-0.25 |
| Diamètre de la tache focale | dU | µm | 1-10 | 0.1-10 |
| Augmentation de l'intensité | K | 1 | 5-100 | 5-1000 |
Tableau 2 : Paramètres typiques des plaques de zone réfléchissantes de Fresnel [VDI 2009d].

Fig. 7 : Schéma de la fonction d'une plaque de zone de Bragg-Fresnel réfléchissante
Plaques de zone condenseur
Des plaques de zone spéciales servent d'optiques à condenseur pour l'éclairage des échantillons dans les microscopes à rayons X à transmission. Dans ce cas, il est important d'éclairer une surface carrée ou rectangulaire sur l'échantillon de manière aussi homogène et lumineuse que possible. La distance b entre le condenseur et le plan éclairé, la taille du condenseur et la taille de la zone éclairée Dzone doivent être adaptées à l'ouverture numérique et au champ de vision de l'optique microscopique. La figure 8 [Jef 2008] montre une conception de condenseur appropriée (du PSI).

Fig. 8 : Croquis d'une plaque de zone de condenseur pour l'éclairage d'un champ d'image carré
Une plaque de zone de condenseur carrée (par ex. 1 mm2) se compose de plusieurs réseaux carrés de la taille du champ d'images (par ex. 20 x 20 réseaux, de 50 x 50 µm2 chacun). Chaque réseau ne comporte que des lignes parallèles et une constante de réseau fixe. Les lignes du réseau sont perpendiculaires à la ligne de raccordement (la ligne a la longueur LZone) du centre du réseau respectif au centre de la plaque de zone. La constante du réseau gZone du réseau respectif est pour une plaque de zone de condenseur fonctionnant dans le premier ordre de diffraction.
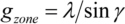
avec (fig. 9)
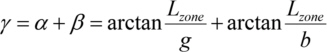
Si ces conditions sont remplies, la lumière de l'un des champs du réseau est diffractée dans le champ d'image de l'échantillon.
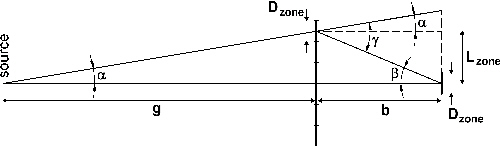
Fig. 9 : Angle pour le calcul d'une plaque de zone du condenseur
| [Fre 1866] | A. J. Fresnel, "Calcul de l'intensité de la lumière au centre de l'ombre d'un ecran et d'une ouverture circulaires eclairés par un point radieux", in: Œuvres Complètes d'Augustin Fresnel, Imprimerie Impériale, Paris, 1866 |
| [Jef 2008] | K. Jefimovs, J. Vila-Comamala, M. Stampanoni, B. Kaulich, C. David, Beamshaping Condenser Lenses for Full-Field Transmission X-ray Microscopy, Journal of Synchrotron Radiation 15, p. 106-108, 2008 |
| [Kip 2001] | L. Kipp, M. Skibowski, R. L. Johnson, R. Berndt, R. Adelung, S. Harm, and R. Seemann, Sharper images by focusing soft X-rays with photon sieves, Nature, 414, 184, DOI: 10.1038/35102526, 2001 |
| [Sor 1875] | J. Soret, Über die durch Kreisgitter erzeugten Diffraktionsphänomene, Annalen der Physik und Chemie 156, p. 99-113, 1875 |
| [VDI 2009c] | VDI/VDE 5575 Blatt 5:2009-02 Röntgenoptische Systeme, Transmissionszonenplatten (X-ray optical systems; Transmission zone plates), Berlin, Beuth Verlag, 2009 |
| [VDI 2009d] | VDI/VDE 5575 Blatt 6:2009-03 Röntgenoptische Systeme, Reflexionszonenplatten (X-ray optical systems; Reflexion zone plates), Berlin, Beuth Verlag, 2009 |


