Les rayons X sont réfléchis par les surfaces dans certaines conditions. Habituellement, on distingue trois types de réflexion :
| Réflexion externe totale | Réflexion de Bragg | Réflexion multicouche |
Réflexion externe totale
Lorsque les rayons X pénètrent dans la matière sous incidence rasante, ils sont réfléchis par réflexion externe totale (TER) lorsque l'angle d'incidence est inférieur à l'angle critique αcritical.
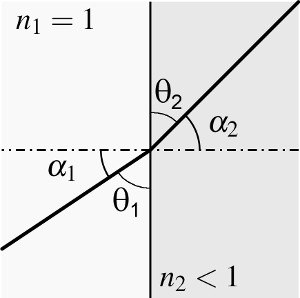
Fig. 1 : Croquis montrant les angles et indices de réfraction utilisés
pour calculer l'angle critique de la réflexion externe totale
L'angle critique peut être calculé comme suit (voir fig. 1). D'après la réfraction des rayons X, nous savons que la loi de Snell est la suivante
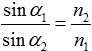
avec l'angle α1 du rayon entrant et α2 du rayon sortant et les indices de réfraction n2 dans la matière et n1 dans le milieu dont provient le rayon. La réflexion externe totale se produit pour les angles α1, lorsque l'angle α2 atteint 90°. En supposant que le rayon provient du vide, n1=1. L'angle critique de αcritical est donc le suivant
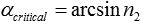
Comme n2 n'est que légèrement inférieur à un (par exemple pour l'or pour des énergies photoniques de 12,4 keV, n2 = 1 - 1,88·10-5), l'angle maximal de TER est proche de 90° (pour l'or à 12,4 keV αcritical = 89,65° = 90°-0,351°). Pour les rayons X, la réflexion externe totale ne se produit qu'en cas d'incidence rasante. Ainsi, les angles de réflexion α sont toujours proches de 90°. Par conséquent, les angles de réflexion sont normalement mesurés entre l'angle du rayon entrant et la surface des miroirs. L'angle critique θcritical est alors
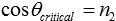
avec n2 = 1-δ et avec l'expansion de Taylor du cosinus
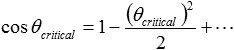
l'angle critique θcritical est
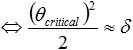
ou
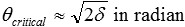
ou en multipliant avec 180/π
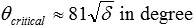
Cette approximation résulte en une erreur inférieure à 0,021% pour θcritical<1°. Dans l'exemple de l'or et d'une énergie photonique de 12,4 keV, θcritical =0,351°. La réflexion externe totale est presque, mais pas complètement sans perte, car le coefficient d'absorption β n'est pas nul.
Réflexion de Bragg
Les surfaces cristallines montrent une réflectivité élevée sous des angles spéciaux en fonction de la longueur d'onde des rayons X due à la réflexion de Bragg. Les miroirs utilisant la réflexion de Bragg pour rediriger les rayons X sont appelés miroirs cristallins. Ces miroirs fournissent de grands angles de réflexion lorsque la condition de réflexion pour une longueur d'onde donnée est remplie. Pour comprendre le principe physique, on considère la différence de trajet d'un rayon entrant réfléchi à la surface d'un cristal et d'un rayon voisin réfléchi à la couche atomique intérieure suivante (voir figure 2). Lorsque la différence de chemin optique
Δ=2d sinθ
avec la distance d entre deux couches atomiques adjacentes et l'angle θ de l'onde entrante mesurée vers la surface est un multiple entier m de la longueur d'onde λ, une interférence constructive survient et l'onde est donc réfléchie. C'est ce qu'on appelle l'équation de Bragg :
mλ=2d sinθ
La réflexion de Bragg est utilisée par exemple pour focaliser le faisceau monochromatique avec des miroirs cristallins courbés elliptiquement et dans les monochromateurs pour filtrer les longueurs d'onde et en science des matériaux pour calculer les constantes de réseau atomique d à partir des angles de réflexion des échantillons cristallins.
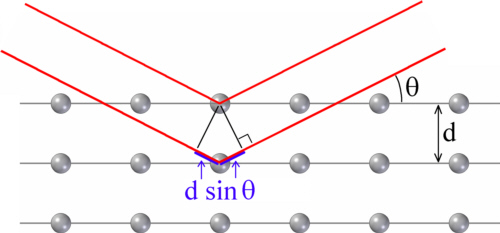
Fig. 2 : Réflexion de Bragg ; lorsque la différence de trajet optique Δ=2d sinθ pour une certaine longueur d'onde λ est un multiple de λ, les faisceaux interfèrent de manière constructive.
Réflexion multicouche
Un miroir à rayons X peut être formé en fabriquant un système multicouche composé de couches d'indices de réfraction différents (voir fig. 3).
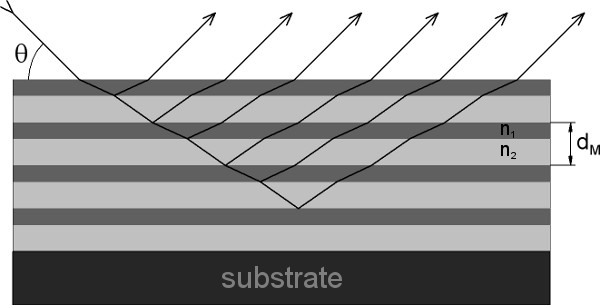
Fig. 3 : Réflexion des rayons X sur un miroir multicouche
L'équation de Bragg change alors pour compenser la réfraction dans les couches [Tho 2009] :
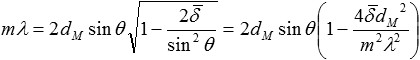
avec l'ordre m, la longueur d'onde λ, la période dM du système multicouche, l'angle d'incidence θ et la partie réelle ![]() de l'indice de réfraction moyenné sur la période du système multicouche.
de l'indice de réfraction moyenné sur la période du système multicouche.
| [Tho 2009] |
A. C. Thompson, J. Kirz, D. T. Attwood, E. M. Gullikson, M. R. Howells, J. B. Kortright, Y. Liu and A. L. Robinson; X-ray data booklet, third edition, Lawrence Berkeley National Laboratory, Berkeley, California, 2009 |


